vectorizing a gotoBLAS/BLIS 8x8 sgemm kernel
for a general introduction into sgemms, check out this and this. Note this is not official gotoBLAS/BLIS code. It is an 8x8 AVX256 implementation of their paper. All examples are running on ubuntu 22.04.3 and compiled with g++ 11.4.0
we define the following type as wrapper over AVX registers in order to access specific floats:
typedef union {
__m256 v;
float f[8];
} m256_t;function
we take in templates mb, kb as the block sizes, th number of threads, m rows of a, n columns of b and k shared dimension. We also take in arguments a and b as the matrices to be multiplied, c as the matrix to be populated and lda, ldb, ldc as the stride length of their respective matrices:
template <int mb, int kb, int th, int m, int n, int k>
void sgemm(float* a, float* b, float* c, int lda, int ldb, int ldc) {
// . . .
} the function expects all matrix data to be aligned in memory, otherwise it segfaults:
float* a = new alignas(32) float[N*N]; // g++
float* a = new float[N*N] alignas(32); // clang blocking
one of the main bottlenecks we encounter is memory bandwidth. Modern CPUs have 3 levels of SRAM, L1, L2, L3, DRAM and then disk. Memory access speeds slow down as you go down the chain and memory size shrinks as you go up. On my CPU, a ryzen 3900X :
| memory | latency | associativity | size | f32 |
|---|---|---|---|---|
| L1 | ~4 cycles | 8-way | 32kB /core | ~8000 /c |
| L2 | ~12 cycles | 8-way | 512kB /core | ~128.000 /c |
| L3 | ~47 cycles | 16-way | 64MB shared | ~16.384.000 |
| DRAM | ~47c+74ns | ~ | ~ | ~ |
| NVMe | ~25.000ns | ~ | ~ | ~ |
| SATA | ~100.000ns | ~ | ~ | ~ |
Minimising slower memory use leads to a faster runtime.
cpuid cache information
in order to find cpu cache information, you can execute a cpuid instruction with eax set to 0x1, 0x2 on intel, and 0x800000005, 0x800000006 on amd. read more about it here or read the working example in tensorlib. to call it use inline assembly:
void _cpuid(long int op, uint32_t& eax, uint32_t& ebx,
uint32_t& ecx, uint32_t& edx) {
asm volatile (
"cpuid"
: "=a"(eax), "=b"(ebx), "=c"(ecx), "=d"(edx)
: "a"(op)
: "cc"
);
}
the first step is to divide the big matrices into sub-matrices of a given block size that can fit into smaller, faster memory. In the BLIS paper, the authors aim to keep the current block of b in L3 and the current block of a mainly in L2. Because of this, the pack of b is bigger. On my CPU, we should be allowed ~15.000.000 f32's for b and ~1.500.000 f32's for a, if we use all 12 cores.
for(int i=0; i<k; i+=kb) {
int ib = std::min(k-i, kb);
for(int ii=0; ii<m; ii+mb) {
int iib = std::min(m-ii, mb);
// . . .
}
}
we iterate over the shared dimension k and m rows of a. i and ii are the block indexes and ib, iib are the current running block sizes (in case k or m are not divisible by kb or mb)
We create pointers wa and wb to point to the current block:
float* wa = &a[i*lda+ii];
float* wb = &b[i];
float* tc = &c[ii];consider the matrices a and b to be 32x32 and blocks kb and mb to be 8. b and c are split into column panels of sizes kb x k (8x32) and mb x m (8x32) starting at index &b[i] and &c[ii] respectively:
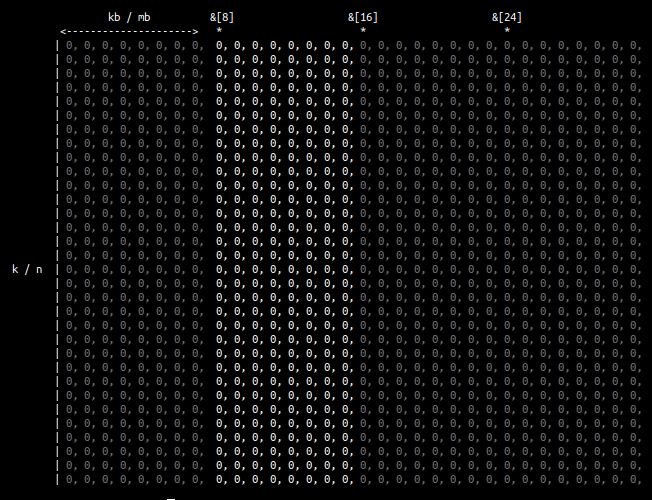
a is split into kb x mb (8x8) blocks starting at row i and column ii:

packing
the first sub-matrix of a in the image above is not contiguous in memory. To get to the second row, you need to skip 24 values. As the matrix size gets bigger, the number of elements you have to skip get larger. You start getting cache misses and TLB misses. To avoid this, and get the benefit of contiguous memory, we pack the current blocks of a and b into buffers.
about TLB misses and CPU halts
TODO
Adding more reads and writes to optimise is counter-intuitive, but as pointed out in this paper, the cost needs not to create a substantial overhead beyond what is already exposed from the loading [...] into the L2 cache and TLB.
we allocate the packs:
float* pa = new alignas(32) float[ib*iib];
float* pb = new alignas(32) float[iib*n];in order to pack a, we loop over block size ib:
inline void pack_a(int ib, const float* a, int lda, float* to) {
for(int i=0; i<ib; i++) {
const float* a_ij_ptr = &a[i*lda];
*to = *a_ij_ptr;
*(to+1) = *(a_ij_ptr+1);
*(to+2) = *(a_ij_ptr+2);
*(to+3) = *(a_ij_ptr+3);
*(to+4) = *(a_ij_ptr+4);
*(to+5) = *(a_ij_ptr+5);
*(to+6) = *(a_ij_ptr+6);
*(to+7) = *(a_ij_ptr+7);
to += 8;
}
} consider that the block size is now 16 and below is the first block of a. A call to pack_a copies the first 8 values of each row of the block contiguously into the pack:
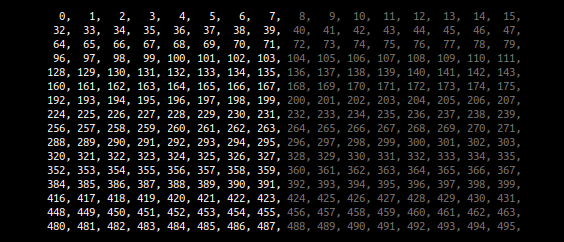
the pack looks like this:

below are the first 16 rows of the block of b. A call to pack_b copies all columns of the first 8 rows of the block into a buffer:

because of this, we can order the elements of b column-major and skip an explicit transposition:
inline void pack_b(int ib, const float* b, int ldb, float* to) {
const float *b_i0_ptr = &b[0],
*b_i1_ptr = &b[(1*ldb)],
*b_i2_ptr = &b[(2*ldb)],
*b_i3_ptr = &b[(3*ldb)],
*b_i4_ptr = &b[(4*ldb)],
*b_i5_ptr = &b[(5*ldb)],
*b_i6_ptr = &b[(6*ldb)],
*b_i7_ptr = &b[(7*ldb)];
for(i=0; i<ib; i++) {
*to = *b_i0_ptr;
*(to+1) = *b_i1_ptr;
*(to+2) = *b_i2_ptr;
*(to+3) = *b_i3_ptr;
*(to+4) = *b_i4_ptr;
*(to+5) = *b_i5_ptr;
*(to+6) = *b_i6_ptr;
*(to+7) = *b_i7_ptr;
to += 8;
b_i0_ptr++; b_i1_ptr++;
b_i2_ptr++; b_i3_ptr++;
b_i4_ptr++; b_i5_ptr++;
b_i6_ptr++; b_i7_ptr++;
}
} a full pack of b looks like this:
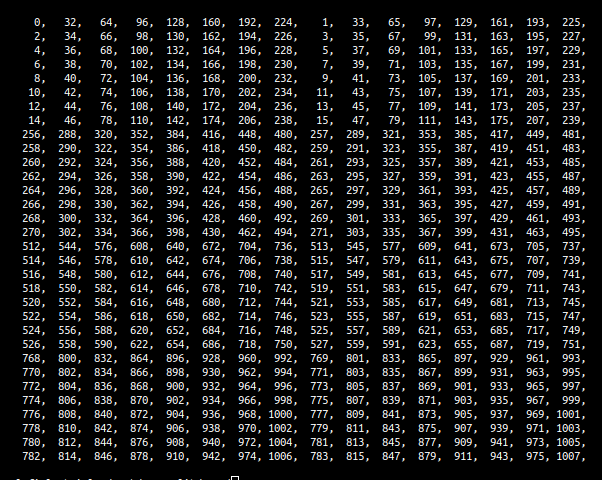
the packing functions are designed only to move as many values as we can pass in a single call to the 8x8 kernel. To prepare for the next kernel call, we call them again while incrementing the starting index of a by 8 and of b by 8*ldb.
kernel control flow
we're blocking the matrices into sub-matrices, now we need to split the sub-matrices into 8x8 blocks to pass them into the kernel.
for(int iii=0; iii<n; iii+=8) {
if(ii==0) pack_b(ib, &wb[iii*n], n, &pb[iii*ib]);
for(int iiii=0; iiii<iib; iiii+=8) {
if(iii==0) pack_a(ib, &wa[iiii], k, &pa[iiii*ib]);
// 8x8 kernel . . .
}
} consider a 32x32 matrix with 16x16 blocks updated by the 8x8 kernel. one single run of the kernel updates an 8x8 panel of c:
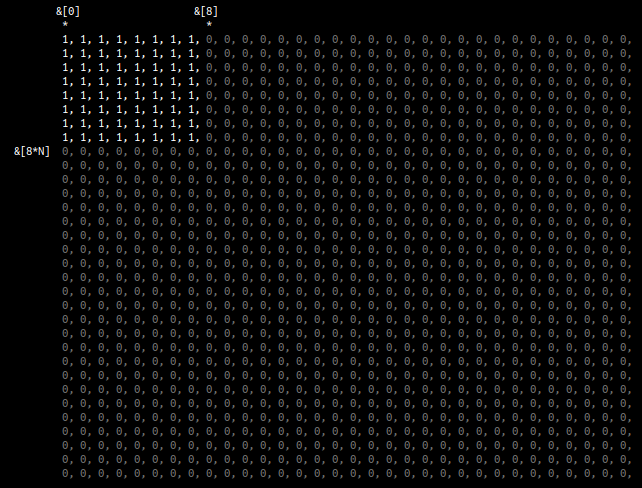
running the iiii loop iterates the 8x8 kernel over the columns of c until it reaches the block size. in the image below, the kernel ran 2 times equaling a 16x8 panel of c being updated:

at the same time, we have filled pa with all the values of the first 16x16 block. Each run of the iiii loop first packs the relevant 8x16 of a then passes the packed values into the kernel. The entire pack of a is shown below, with each element's value equal to it's index in a:


running the iii loop iterates the 16x8 panel over all rows of c, updating a 16xm panel of c. in this case, it happens to be half:

while this loop runs, we also fill pb in the same manner:

the ii loop completes the first run over c in panels of 16xm:
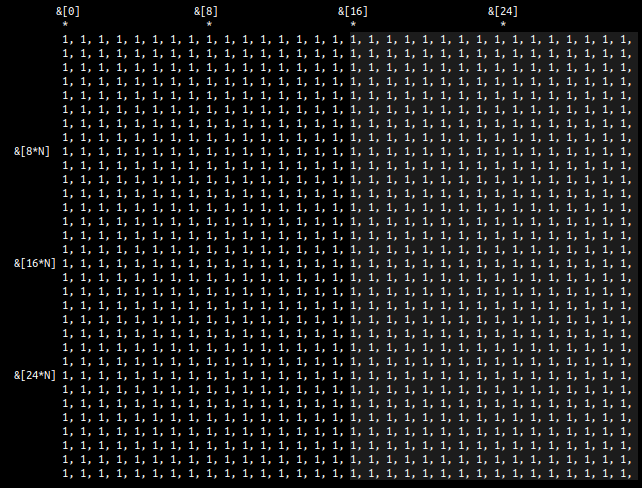
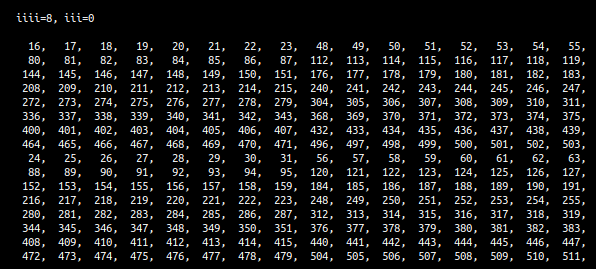
for every iteration of this loop, we change the packed values of a. The next ones are:
finally, the i loop compounts all values of c to their correct end value. For every iteration of this loop, we change the packed values of b.
8x8 kernel
the rest is easy, we only concern ourselves with the contigous packs of a and b and pick 8 values at a time from both to multiply
we define workin pointers wpa and wpb into their respective packs. notice the index is the same as the beginning of the current sub-block moved in the same loop. wc points to the beginning of the 8x8 panel we will update in c.
float* wpa = &pa[iiii*ib];
float* wpb = &pb[iii*ib];
float* wc = &tc[iii*n+iiii]; we also define 8 __m256 registers to hold the 64 computed values of c, alongside two registers to hold the data in the packs.
m256_t c0007, c1017, c2027, c3037,
c4047, c5057, c6067, c7077,
a_vreg, b_p0_vreg; set all elements of the c registers to 0:
c0007.v = _mm256_setzero_ps();
c1017.v = _mm256_setzero_ps();
c2027.v = _mm256_setzero_ps();
c3037.v = _mm256_setzero_ps();
c4047.v = _mm256_setzero_ps();
c5057.v = _mm256_setzero_ps();
c6067.v = _mm256_setzero_ps();
c7077.v = _mm256_setzero_ps();if we don't do this, they keep their values into the next loop. we also cannot do this at the end of the loop, because the compiler optimises it out.
next we iterate through the 8xib panel we packed before, reading 8 values of pa into a_vreg and 8 values of pb into b_p0_vreg, incrementing the pointers afterwards:
for(iiiii=0; iiiii<iib; iiiii++) {
__builtin_prefetch(wpa+8);
__builtin_prefetch(wpb+8);
a_vreg.v = _mm256_load_ps( (float*) wpa );
wpa += 8;
b_p0_vreg.v = _mm256_load_ps( (float*) wpb);
wpb += 8;
c0007.v += a_vreg.v * b_p0_vreg.f[0];
c1017.v += a_vreg.v * b_p0_vreg.f[1];
c2027.v += a_vreg.v * b_p0_vreg.f[2];
c3037.v += a_vreg.v * b_p0_vreg.f[3];
c4047.v += a_vreg.v * b_p0_vreg.f[4];
c5057.v += a_vreg.v * b_p0_vreg.f[5];
c6067.v += a_vreg.v * b_p0_vreg.f[6];
c7077.v += a_vreg.v * b_p0_vreg.f[7];
}we multiply all the 8 values of a_vreg with one single value of b_p0_vreg and accumulate it in the c registers.
notice we don't explicitly call _mm256_fmadd_ps. This is because both of the arguments would need to be __mm256 registers. the code would look like this:
m256_t b0, b1, b2, b3, b4, b5, b6, b7;
b0.v = _mm256_broadcast_ss( (float*) &wpa[0] );
b1.v = _mm256_broadcast_ss( (float*) &wpa[1] );
b2.v = _mm256_broadcast_ss( (float*) &wpa[2] );
b3.v = _mm256_broadcast_ss( (float*) &wpa[3] );
b4.v = _mm256_broadcast_ss( (float*) &wpa[4] );
b5.v = _mm256_broadcast_ss( (float*) &wpa[5] );
b6.v = _mm256_broadcast_ss( (float*) &wpa[6] );
b7.v = _mm256_broadcast_ss( (float*) &wpa[7] );
c0007.v = _mm256_fmadd_ps(a_vreg.v, b0.v, c0007.v);
c1017.v = _mm256_fmadd_ps(a_vreg.v, b1.v, c1017.v);
c2027.v = _mm256_fmadd_ps(a_vreg.v, b2.v, c2027.v);
c3037.v = _mm256_fmadd_ps(a_vreg.v, b3.v, c3037.v);
c4047.v = _mm256_fmadd_ps(a_vreg.v, b4.v, c4047.v);
c5057.v = _mm256_fmadd_ps(a_vreg.v, b5.v, c5057.v);
c6067.v = _mm256_fmadd_ps(a_vreg.v, b6.v, c6067.v);
c7077.v = _mm256_fmadd_ps(a_vreg.v, b7.v, c7077.v); we use _mm256_broadcast_ss to fill the b* registers with the relevant float of b and then perform _mm256_fmadd_ps, multiplying a_vreg with b* register and adding the previous value of the relevant c register
in theory, this is the most efficient way to do this. in practice, we already use 9 ymm registers allocated by our previous declaration of the __m256 types:
m256_t c0007, c1017, c2027, c3037,
c4047, c5057, c6067, c7077,
a_vreg; with the addition of another 8, this puts us at 17. my processor, similar to a lot of modern processors, only has 16 physical ymm registers on the chip. explicitly defining the 8 b registers would introduce data movement in the most important part of the code, forcing it to allocate and dealocate ymm registers to new values.
taking a look at the compiled files lets us see that the behaviour of both solutions is very similar. the compiler uses _mm256_broadcast_ss and _mm256_fmadd_ps anyway.
inner kernel loop with explicit _mm256_broadcast_ss call:
1a30: c5 fc 28 00 vmovaps (%rax),%ymm0
1a34: 48 83 c0 20 add $0x20,%rax
1a38: 49 83 c0 20 add $0x20,%r8
1a3c: c4 62 7d 18 70 04 vbroadcastss 0x4(%rax),%ymm14
1a42: c4 62 7d 18 38 vbroadcastss (%rax),%ymm15
1a47: 0f 18 08 prefetcht0 (%rax)
1a4a: 41 0f 18 08 prefetcht0 (%r8)
1a4e: c4 62 7d a8 b4 24 20 vfmadd213ps 0x120(%rsp),%ymm0,%ymm14
1a55: 01 00 00
1a58: c4 62 7d 18 68 08 vbroadcastss 0x8(%rax),%ymm13
1a5e: c4 62 7d 18 60 0c vbroadcastss 0xc(%rax),%ymm12
1a64: c4 62 7d 18 58 10 vbroadcastss 0x10(%rax),%ymm11
1a6a: c4 62 7d 18 50 14 vbroadcastss 0x14(%rax),%ymm10
1a70: c4 62 7d 18 48 18 vbroadcastss 0x18(%rax),%ymm9
1a76: c4 e2 7d 18 48 1c vbroadcastss 0x1c(%rax),%ymm1
1a7c: c4 42 7d b8 c7 vfmadd231ps %ymm15,%ymm0,%ymm8
1a81: c4 c2 7d b8 d5 vfmadd231ps %ymm13,%ymm0,%ymm2
1a86: c4 c2 7d b8 dc vfmadd231ps %ymm12,%ymm0,%ymm3
1a8b: c4 c2 7d b8 e3 vfmadd231ps %ymm11,%ymm0,%ymm4
1a90: c4 c2 7d b8 ea vfmadd231ps %ymm10,%ymm0,%ymm5
1a95: c4 c2 7d b8 f1 vfmadd231ps %ymm9,%ymm0,%ymm6
1a9a: c4 e2 7d b8 f9 vfmadd231ps %ymm1,%ymm0,%ymm7
1a9f: c5 7c 29 b4 24 20 01 vmovaps %ymm14,0x120(%rsp)
1aa6: 00 00
1aa8: 48 39 f8 cmp %rdi,%rax
1aab: 75 83 jne 1a30 <_Z5sgemm . . . >
the highlighted part calls vfmadd213ps with the first opperand as a relative address to the rsp stack pointer. It multiplies ymm0 with the 8 subsequent values from the rsp pointer, adds the values from ymm14 and stores in the rsp stack variable, not in a ymm register. This small change costs us ~25% of the final performance.
inner kernel loop without explicit intrinsics:
1a00: c4 c1 7c 28 00 vmovaps (%r8),%ymm0
1a05: c5 fc 28 08 vmovaps (%rax),%ymm1
1a09: 49 83 c0 20 add $0x20,%r8
1a0d: 48 83 c0 20 add $0x20,%rax
1a11: 0f 18 08 prefetcht0 (%rax)
1a14: 41 0f 18 08 prefetcht0 (%r8)
1a18: c4 e2 7d 18 c0 vbroadcastss %xmm0,%ymm0
1a1d: c4 e2 75 b8 d0 vfmadd231ps %ymm0,%ymm1,%ymm2
1a22: c4 c2 7d 18 40 e4 vbroadcastss -0x1c(%r8),%ymm0
1a28: c4 e2 75 b8 d8 vfmadd231ps %ymm0,%ymm1,%ymm3
1a2d: c4 c2 7d 18 40 e8 vbroadcastss -0x18(%r8),%ymm0
1a33: c4 e2 75 b8 e0 vfmadd231ps %ymm0,%ymm1,%ymm4
1a38: c4 c2 7d 18 40 ec vbroadcastss -0x14(%r8),%ymm0
1a3e: c4 e2 75 b8 e8 vfmadd231ps %ymm0,%ymm1,%ymm5
1a43: c4 c2 7d 18 40 f0 vbroadcastss -0x10(%r8),%ymm0
1a49: c4 e2 75 b8 f0 vfmadd231ps %ymm0,%ymm1,%ymm6
1a4e: c4 c2 7d 18 40 f4 vbroadcastss -0xc(%r8),%ymm0
1a54: c4 e2 75 b8 f8 vfmadd231ps %ymm0,%ymm1,%ymm7
1a59: c4 c2 7d 18 40 f8 vbroadcastss -0x8(%r8),%ymm0
1a5f: c4 62 75 b8 c0 vfmadd231ps %ymm0,%ymm1,%ymm8
1a64: c4 c2 7d 18 40 fc vbroadcastss -0x4(%r8),%ymm0
1a6a: c4 62 75 b8 c8 vfmadd231ps %ymm0,%ymm1,%ymm9
1a6f: 48 39 f8 cmp %rdi,%rax
1a72: 75 8c jne 1a00 <_Z5sgemm . . . >
we only end up using one register, ymm0 to broadcast the values of b. this is good because we never intended to reuse the allocated b* registers.
lastly we just have to update c. Because we are out of the innermost loop and don't care about the values anymore, we are ok with realocating ymm registers. We define 8 __m256 registers to hold the previous values stored in c and load:
m256_t w0, w1, w2, w3, w4, w5, w6, w7;
w0.v = _mm256_load_ps((float*)&wc[0*ldc]);
w1.v = _mm256_load_ps((float*)&wc[1*ldc]);
w2.v = _mm256_load_ps((float*)&wc[2*ldc]);
w3.v = _mm256_load_ps((float*)&wc[3*ldc]);
w4.v = _mm256_load_ps((float*)&wc[4*ldc]);
w5.v = _mm256_load_ps((float*)&wc[5*ldc]);
w6.v = _mm256_load_ps((float*)&wc[6*ldc]);
w7.v = _mm256_load_ps((float*)&wc[7*ldc]);
then, we add the newly computed values to the old values using _mm256_add_ps and store them again at the same location in c:
c0007.v = _mm256_add_ps(c0007.v, w0.v);
c1017.v = _mm256_add_ps(c1017.v, w1.v);
c2027.v = _mm256_add_ps(c2027.v, w2.v);
c3037.v = _mm256_add_ps(c3037.v, w3.v);
c4047.v = _mm256_add_ps(c4047.v, w4.v);
c5057.v = _mm256_add_ps(c5057.v, w5.v);
c6067.v = _mm256_add_ps(c6067.v, w6.v);
c7077.v = _mm256_add_ps(c7077.v, w7.v);
_mm256_store_ps( &wc[0*ldc], c0007.v);
_mm256_store_ps( &wc[1*ldc], c1017.v);
_mm256_store_ps( &wc[2*ldc], c2027.v);
_mm256_store_ps( &wc[3*ldc], c3037.v);
_mm256_store_ps( &wc[4*ldc], c4047.v);
_mm256_store_ps( &wc[5*ldc], c5057.v);
_mm256_store_ps( &wc[6*ldc], c6067.v);
_mm256_store_ps( &wc[7*ldc], c7077.v);
_mm256_store_ps, just like _m256_load_ps works on the 8 32-bit values following the starting pointer. We end up reading and updating 64 values in an 8x8 panel of c.
performance
running on ubuntu 22.04.3 and compiled with g++ 11.4.0
CPU: Ryzen 9 3900X 12 core, 4.6 GHz
DRAM: 128 GB 3200 MHz, dual channel
| N | block | threads | iterations | runtime | GFLOPS |
|---|---|---|---|---|---|
| 512 | 64 | 12 | 1000 | 1.11ms | 241.30 |
| 1024 | 128 | 12 | 1000 | 5.34ms | 401.89 |
| 2048 | 256 | 12 | 1000 | 33.27ms | 516.12 |
| 4096 | 512 | 12 | 100 | 222.39ms | 618.00 |
| 8192 | 1024 | 12 | 10 | 1664.49ms | 660.59 |
on explicit transposition
because the packing we do does not add any substancial overhead, starting out with a transposed b would not improve the runtime. Quite the oposite, the added runtime of the transposition kernel ends up costing us ~1-2ms for N=1024.
notes
find the full code here